Algebra

Introduction to Algebraic Expressions and Identities

Algebraic Expressions

Algebraic expressions are expressions made up of variables and constants along with mathematical operators. Algebraic expressions have no sides or equal to sign like algebraic equations.
Examples of algebraic expressions are: 2x + 4, 7y - 3 + 6x, 3t² + 4t - 1.

Terms

Terms are the individual building blocks of expressions. They add up to form expressions. A term is a product of its factors.

Example

For example, the expression 5xy - 3 is made up of two terms, 5xy and (-3).

Factors

Factors are those variables or constants, whose product form a term of an expression.

Example

8, p and q are the factors of the term 8pq.
Factors are such that they cannot be factorised further.

The product of factors forms a term and the summation of the terms forms an expression.

Coefficients

The numerical factor of a term is called the coefficient of that term.

Example

For the terms 6y and 2xy, the coefficient of 6y is 6 and the coefficient of 2xy is 2.

Like Terms

Like terms are those terms which have the same variables raised to the same power. Like terms have the same algebraic factors. The numerical coefficient of like terms can be different.

Example

3x²y and 5x²y are like terms.

Monomial

An expression with only one term is called a monomial.

Examples

6x, 7pq, x²y, 9xyz, 4bc

Binomial

An expression which contains two unlike terms is called a binomial.

Examples

4y - 3z, x⁶ - 2, pq + 1

Polynomial

Expressions that have more than two terms with non-zero coefficients and variables having non-negative integral exponents are called polynomials.

Examples

a + b + c + 2, 7xy - 8x + 2 + 3y, 5t³ - 7t + k + 3

Algebraic Identities

• (a + b)² = a² + 2ab + b²
• (a - b)² = a² - 2ab + b²
• (a + b)(a - b) = a² - b²

Addition and Subtraction of Algebraic Expressions

When we are adding or subtracting two algebraic expressions, we can only add or subtract like terms. The sum of two or more like terms is a like term, with a numerical coefficient equal to the sum of the numerical coefficient of all the like terms.

Similarly, the difference between two like terms is a like term with a equal to the difference between the numerical coefficients of the two like terms.

Suppose if we have to add 3x²y+y+z and 4x²y+7a+5z, we will combine all the like terms and then add their numerical coefficients.
= (3x²y + 4x²y) + (y) + (7a) + (z + 5z)
= 7x²y + y + 7a + 6z

Multiplication of Algebraic Expressions

Multiplication of Monomials

When we multiply two monomials:

• the numerical coefficient of the terms is equal to the product of the numerical coefficient of both the terms.
• the exponent or power of each algebraic factor is equal to the sum of the exponents of that algebraic factor in both the monomials.

Multiplying two monomials:

• x × 3y = x × 3 × y = 3 × x × y = 3xy
• 3x × 2y = 3 × x × 2 × y = 3 × 2 × x × y = 6xy
• 5x × (−2z) = 5 × (−2) × x × z = −10xz

Multiplying three or more monomials:

• 2x × 3y × 5z = (2x × 3y) × 5z = 6xy × 5z = 30xyz
• 4xy × 5x²y² × 6x³y³ = (4xy × 5x²y²) × 6x³y³ = 20x³y³ × 6x³y³ = 120x⁶y⁶

Distributive Property of Multiplication

The distributive property is an algebraic property that is used to multiply a single value and two or more values within a set of parenthesis.
Consider the expression : 6 × (2 + 4x)
Consider the expression= (6 × 2) + (6 × 4x)
Consider the expression= 12 + 24x
Here, we have used distributive law to mutiply a monomial and a binomial.

Multiplication of any Polynomial

When we multiply any two polynomials, we multiply all the terms or monomials of one polynomial with all the terms of another polynomial.

When we multiply two binomials, every term in one binomial multiplies every term in the other binomial.

= (3a + 4b) × (2a + 3b)
= 3a × (2a + 3b) + 4b × (2a + 3b)
= (3a × 2a) + (3a × 3b) + (4b × 2a) + (4b × 3b)
= 6a² + 9ab + 8ab + 12b²
= 6a² + 17ab + 12b²

When we multiply a binomial by a trinomial, each of the three terms of the trinomial is multiplied by each of the two terms of the binomial.

• Multiplying a binomial by a trinomial

= (p + 4) × (p² + 2p + 3)
= p × (p² + 2p + 3) + 4 × (p² + 2p + 3)
= (p³ + 2p² + 3p) + (4p² + 8p + 12)
= p³ + 6p² + 11p + 12

Factorization

What are Factors?

An expression can be factorised into the product of its factors. These factors can be algebraic expressions, variables and numbers also.

Division of a monomial by another monomial

I) Division of 9x2 by 3:
9x23 = 3(3x2)3 = 3x2

II) Division of 6x2y by 2y:
6x2y2y = (6x2)y2y = 2y(3x2)2y = 3x2

Division of a polynomial by a monomial

A polynomial 2x³ + 4x² + 6x is divided by monomial 2x as shown below:
(2x³ + 4x² + 6x)2x = 2x³2x + 4x²2x + 6x2x = x² + 2x + 3

Division of a polynomial by a polynomial

Long division method is used to divide a polynomial by a polynomial.
Example:Division of 3x² + 3x – 5 by (x – 1) is shown below:

Let's break it down:

1. We divide the first term of the dividend 3x³ by the first term of the divisor x, which gives 3x². That’s the first term in the quotient.
2. Multiply the entire divisor (x − 1) by 3x²: 3x² × (x − 1) = 3x³ − 3x².
3. Subtract that from the dividend:
   (3x³ + 0x² − 8x + 5) − (3x³ − 3x²) = 3x² − 8x + 5
4. Repeat the process: divide 3x² by x, getting +3x. Multiply: 3x × (x − 1) = 3x² − 3x. Subtract: (3x² − 8x + 5) − (3x² − 3x) = −5x + 5
5. Divide −5x by x, getting −5. Multiply: −5 × (x − 1) = −5x + 5. Subtracting gives 0, which means no remainder.

Factors of natural numbers

Every number can be expressed in the form of product of prime factors. This is called prime factor form.

Example: Prime factor form of 42 is 2 x 3 x 7, where 2, 3 and 7 are factors of 42.

Algebraic expressions

An algebraic expression is defined as a mathematical expression which consists of variables, numbers, and operations. The values of this expression are not constant, for example: x + 1, p – q, 3x, 2x + 3y, 5a6b etc.

Factors of algebraic expressions and factorisation

An irreducible factor is a factor which cannot be expressed further as a product of factors.
Algebraic expressions can be expressed in irreducible form.

Method of Common Factors

Factorisation by common factors

To factorise an algebraic expression, the highest common factors are determined.

Example: Algebraic expression -2y² + 8y can be written as 2y(-y+4), where 2y is the highest common factor in the expression.

Factorisation by regrouping terms

In some algebraic expressions, it is not possible that every term has a common factor. Therefore, to factorise those algebraic expressions, terms having common factors are grouped together.

Example:
= 12a + n - na - 12
= 12a - 12 + n - na
= 12(a - 1) - n(a - 1)
= (12 - n)(a - 1)
(12 - n) and (a - 1) are factors of the expression 12a + n - na - 12

Method of Identities

Algebraic identities

The algebraic equations which are true for all values of variables in them are called algebraic identities.

Some of the identities are:
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
(a + b)(a - b) = a² - b²

Factorisation using algebraic identities

Example: (i) 9x² + 12xy + 4y²
Example:()= (3x)² + 2 × 3x × 2y + (2y)²
Example:()= (3x + 2y)²
(ii) 4a² - b²
()= (2a - b)(2a + b)

Visualisation of factorisation

The algebraic expression x² + 8x + 16 can be written as (x + 4)². This can be visualised as shown below:

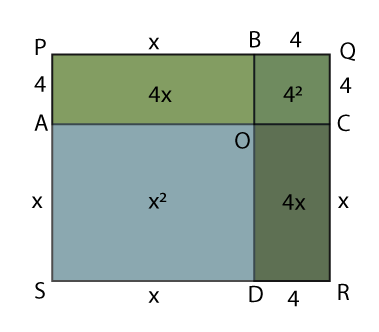
The given figure is a square divided into smaller rectangles and squares. Let's understand each part:

1. The large square has side length x + 4. It is made up of four parts: one square with area x², two rectangles each with area 4x, and one small square with area 4².
2. The square POSD has side length x and hence its area is x².
3. Rectangle PBAO has dimensions x and 4, so its area is 4x.
4. Rectangle ODCR also has dimensions x and 4, so its area is again 4x.
5. The square BOQC has side length 4, so its area is 4².

Hence, the total area of the large square is:

x² + 4x + 4x + 4² = x² + 8x + 16

This visual helps in understanding the expansion of the identity:
(x + 4)² = x² + 8x + 16

Short Answer Questions(SAQs)

What is the Distributive Property?

According to the distributive property, multiplying the sum of two or more addends by a number will give the same result as multiplying each addend individually by the number and then adding the products together.

What are Coefficients?

A coefficient is a number or an alphabet that is multiplied by a variable of a single term or the terms of a polynomial.

What is the definition of Like Terms?

Terms whose variables (such as x or y) with any exponents (such as the 2 in x²) are the same.

What are Factors?

A number or algebraic expression that divides another number or expression evenly—i.e., with no remainder is said to be a factor of the primary number.

What is a common multiple?

A multiple of each of two or more numbers is said to be ‘common mutiple’ of both the numbers.

What is Factorisation?

Factorisation is when a number is broken down into smaller numbers that, multiplied together, give the original number.

MCQs

1. Which of the following is an algebraic expression?

(a) 5 + 3 = 8

(b) x + 5 = 9

(c) 3x + 7

(d) 12 = 4 + 8

► (c) 3x + 7

2. In the expression 4x − 2y + 7, how many terms are there?

(a) 2

(b) 3

(c) 4

(d) 1

► (b) 3

3. Evaluate the expression 2a + 3b for a = 2 and b = 1.

(a) 5

(b) 7

(c) 8

(d) 10

► (b) 7

4. Which expression represents “the sum of a number and its double”?

(a) x + 2x

(b) x + x

(c) 2x + 2x

(d) x − 2x

► (a) x + 2x

5. Simplify the expression: 5x + 3 − 2x + 7.

(a) 7x + 10

(b) 3x + 4

(c) 5x + 10

(d) 3x + 10

► (d) 3x + 10

6. Which of the following is a monomial?

(a) 5x + 3

(b) 2x − 4

(c) 7xy

(d) 3x + y

► (c) 7xy

7. What is the constant term in 3x − 5 + 2y?

(a) 3

(b) −5

(c) 2

(d) 3x

► (b) −5

8. Which of these is not a like term with 2x²?

(a) 5x²

(b) −x²

(c) 3x

(d) 7x²

► (c) 3x

9. What is the value of the expression x² + 3x + 2 when x = 2?

(a) 8

(b) 12

(c) 16

(d) 20

► (c) 16

10. Identify the variable in the expression: 4m + 5n − 3.

(a) 4

(b) m and n

(c) −3

(d) 5

► (b) m and n

11. Which identity is used in (a + b)² = a² + 2ab + b²?

(a) Distributive

(b) Associative

(c) Algebraic Identity

(d) Commutative

► (c) Algebraic Identity

12. (x + 3)² expands to:

(a) x² + 6x + 9

(b) x² + 3x + 9

(c) x² + 9

(d) x² + 6x + 3

► (a) x² + 6x + 9

13. The identity (a − b)² is equal to:

(a) a² − b²

(b) a² + 2ab + b²

(c) a² − 2ab + b²

(d) a² + b²

► (c) a² − 2ab + b²

14. What is the result of (x + 4)(x − 4)?

(a) x² + 16

(b) x² − 8x + 16

(c) x² − 16

(d) x² − 4

► (c) x² − 16

15. Factorise the expression: x² + 5x + 6

(a) (x + 2)(x + 3)

(b) (x + 1)(x + 6)

(c) (x − 2)(x − 3)

(d) (x − 1)(x − 6)

► (a) (x + 2)(x + 3)

16. Which is a factor of x² − 9?

(a) (x − 9)

(b) (x + 3)

(c) (x + 9)

(d) (x + 1)

► (b) (x + 3)

17. What is the factorized form of x² − 2x − 35?

(a) (x − 7)(x + 5)

(b) (x + 7)(x − 5)

(c) (x − 5)(x + 7)

(d) (x + 5)(x + 7)

► (c) (x − 5)(x + 7)

18. Factorise: x² − 81

(a) (x − 81)(x + 1)

(b) (x − 9)(x + 9)

(c) (x − 27)(x + 3)

(d) (x − 8)(x + 8)

► (b) (x − 9)(x + 9)