Mensuration

What is Mensuration?

Mensuration is a branch of mathematics which mainly deals with the study of different kinds of Geometrical shapes along with their area, length, volume and perimeters. It is completely based on the application of both algebraic equations and geometric calculations. The results obtained by the Mensuration are considered very accurate. There are two types of geometric shapes:

Volume of Solids

Volume of a 3D Object

Volume is the space occupied by the three dimensional object. It is a three-dimensional quantity.

Volume of a Cuboid

Volume of a cuboid =l × b × h
where, l is the length, b is the breadth and h is the height of the cuboid.

Volume of a Cube

Volume of a cube =l³
Where, l is the length of the each side of the cube.

Volume of a Cylinder

Volume of the cylinder =πr²h
Where r is the radius of the base and h is the height of the cylinder.

Basics Revisited

Introduction to Mensuration

Mensuration is the study of geometry that deals with the measurement of length, areas and volumes.

Perimeter is the total length or path of a given shape.
Area is the total region covered by the given shape.
Volume is the total space occupied by the given shape.

Identifying Shapes and Areas of Different Regular Figures

Area of a Rectangle: length × breadth
perimeter: 2 × (length + breadth)

Area of Square: side × side
perimeter: 4 × side

Area of Triangle: 12 × (base × height)
perimeter: a + b + c (sum of 3 sides)

Area of Parallelogram: base × height
perimeter: 2 × (length + breadth)

Area of Circle: π × (radius)²
perimeter: 2 × π × radius

Trapezium

Area of Trapezium by Division into Shapes of Known Area

Consider the trapezium where a and b are parallel sides, h is the height. Trapezium is divided into 3 parts : two triangles, one rectangle.
Here h is the height, a and b are 2 parallel sides.
Area of trapezium = Area of 2 triangles + Area of rectangle
[12 × c × h + 12 × d × h] + [a × h]
= [12 × c × h + 12 × d × h] + [12 × 2a × h] [Multiplying and dividing by 2]
= 12 × h (c + d + 2a)
= 12 × h (c + d + a + a)
= 12 × h (b + a) [∵ c + d + a = b]

Area of trapezium = 12 × h × (sum of 2 parallel sides)

Area of Trapezium by Finding the Area of a Triangle of Same Area

The area of the trapezium can be found out by dividing it into a triangle and a polygon.

Consider a trapezium WXYZ. Mark a midpoint A for side XY and join AZ. Cut the trapezium along AZ and obtain a ΔAZY.
Flip the ΔAZY and place it as shown below. Now the new polygon is a triangle.
We know that,
Area of a triangle = 12 × base × height
Substituting the values we get,
Area of a triangle = 12 × (a + b) × h

But the original polygon is a trapezium. So,
Area of a trapezium = 12 × (a + b) × h

Quadrilaterals in General

Area of a General Quadrilateral

Consider a quadrilateral ABCD. Draw diagonal AC. From B and D draw perpendiculars h₁, h₂ to AC.
Area of quadrilateral = Area of triangle ABC + Area of triangle ADC
= 12 × base × height + 12 × base × height
= (12 × AC × h₁) + (12 × AC × h₂) [Where h₁, h₂ are the heights, AC is the base]
= 12 × AC × (h₁ + h₂)
= 12 × d × (h₁ + h₂) [∵ AC is a diagonal d]

∴ Area of a Quadrilateral = 12 × d × (h₁ + h₂)

Area of Rhombus

Area of Rhombus = 12 × d₁ × d₂
where d₁ and d₂ are the diagonals.

Area of Polygons

The area of any given polygon can be found by cutting the polygon into shapes whose area is known and adding the area of these shapes.

Some of the ways to find the area is shown below.

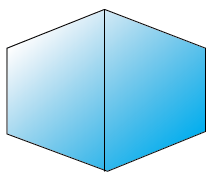
Area of this polygon = Area of 2 trapeziums

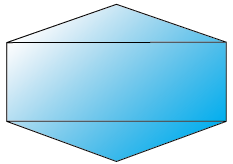
Area of this polygon = Area of 2 triangles + Area of rectangle

Surface Area of Solids

Solid Shapes

Solid shapes or solid figures are the three dimensional figures which have length, breadth and height. Using these, surface areas and volumes of these figures are found out.

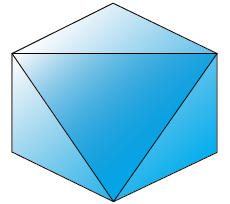
Area of this polygon = Area of 4 triangles

Solids with a Pair or More of Identical Faces

Solids with a pair of identical faces are:

Surface Area of Solid Shapes

The surface area of the object is the total area occupied by the surface of the object.
or surface area is simply the sum of the areas of the flat surfaces (called faces).

Surface Area of a Cuboid

Total Surface Area of cuboid = 2 × (l×b + b×h + l×h)

Lateral Surface Area of cuboid = 2 × h × (l + b)

Where:
l = length,
b = breadth,
h = height

Surface Area of a Cube

Total Surface Area of a cube = 6l²

Lateral Surface Area of a cube = 4l²

Where l is the length of each side of the cube.

Surface Area of a Cylinder

Curved Surface Area (C.S.A) of cylinder = 2πrh

Total Surface Area (T.S.A) of cylinder = 2πr(r + h)

Where:
r = radius of the cylinder,
h = height of the cylinder

Summary of Mensuration

Relation between Volume and Capacity

Volume is the total space occupied by an object. Volume is measured in cubic units,
Capacity refers to the maximum measure of an object’s ability to hold a substance, like a solid, a liquid or a gas. Capacity can be measured in almost every other unit, including liters, gallons, pounds, etc.
Eg : A bucket contains 9 litres of water, then its capacity is 9 litres.

Short Answer Questions(SAQs)

What is the meaning of a Trapezium?

A trapezium (also known as a trapeziod) is a flat 2D shape with four straight sides.

What are the uses of mensuration in daily life?

Paint required to cover a certain area. Volume of soil needed to fill any ditch. Distance around a circular race track.

What is a Pyramid?

Pyramid is a large structure built especially in ancient Egypt that usually has a square base and four triangular sides meeting at a point and that contains tombs.

MCQs

1. What is the formula for the area of a square?

(a) 2 × side

(b) side × side

(c) 4 × side

(d) side + side

► (b) side × side

2. The perimeter of a rectangle is given by:

(a) l × b

(b) 2(l + b)

(c) 2l + b

(d) l + b

► (b) 2(l + b)

3. What is the volume of a cube with edge 4 cm?

(a) 12 cm³

(b) 64 cm³

(c) 16 cm³

(d) 48 cm³

► (b) 64 cm³

4. The area of a triangle is:

(a) base × height

(b) 2 × base × height

(c) 1 2 × base × height

(d) base + height

► (c) 1 2 × base × height

5. Find the volume of a cuboid of length 5 cm, breadth 4 cm and height 3 cm.

(a) 60 cm³

(b) 50 cm³

(c) 12 cm³

(d) 30 cm³

► (a) 60 cm³

6. Surface area of a cube is given by:

(a) 2a²

(b) 6a²

(c) 4a²

(d) a²

► (b) 6a²

7. A cylinder has radius r and height h. Its volume is:

(a) πr²h

(b) 2πr²

(c) πrh

(d) 2πrh

► (a) πr²h

8. A cone has height h and radius r. Its volume is:

(a) πr²h

(b) 1 3 πr²h

(c) 2πr²h

(d) πrh

► (b) 1 3 πr²h

9. What is the curved surface area of a cylinder?

(a) 2πr²

(b) πr²h

(c) 2πrh

(d) πrh

► (c) 2πrh

10. The total surface area of a cube is 150 cm². Find the length of one side.

(a) 5 cm

(b) 10 cm

(c) 6 cm

(d) 7 cm

► (a) 5 cm

11. The perimeter of a square is 36 cm. What is its area?

(a) 81 cm²

(b) 36 cm²

(c) 324 cm²

(d) 49 cm²

► (a) 81 cm²

12. What is the area of a rhombus with diagonals 6 cm and 8 cm?

(a) 24 cm²

(b) 48 cm²

(c) 36 cm²

(d) 28 cm²

► (b) 24 cm²

13. Find the lateral surface area of a cube of side 10 cm.

(a) 200 cm²

(b) 400 cm²

(c) 600 cm²

(d) 800 cm²

► (c) 600 cm²

14. The base area of a cylinder is 154 cm² and height is 10 cm. Find volume.

(a) 1540 cm³

(b) 1500 cm³

(c) 1430 cm³

(d) 1400 cm³

► (a) 1540 cm³

15. What is the volume of a cone with radius 7 cm and height 12 cm? (Use π = 22 7 )

(a) 1232 cm³

(b) 616 cm³

(c) 308 cm³

(d) 600 cm³

► (c) 308 cm³

16. A hemisphere has radius 3.5 cm. Its volume is:

(a) 89.83 cm³

(b) 99.83 cm³

(c) 85.33 cm³

(d) 80.5 cm³

► (a) 89.83 cm³

17. The formula for surface area of a sphere is:

(a) 4πr²

(b) πr²

(c) 2πr²

(d) 3πr²

► (a) 4πr²

18. Which figure has the maximum volume for a given surface area?

(a) Cube

(b) Sphere

(c) Cylinder

(d) Cone

► (b) Sphere